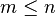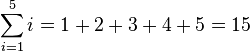martes, 25 de mayo de 2010
Menú
Notación Sigma
Área
Área de una región plana
Cálculo del Área como límite
Integral definida
Ejemplo
Aplicación del tema
Ejemplo
En éste video vemos una explicación paso a paso del cálculo del área de una regiòn bajo la curva, su gráfica, valores, etc mediante la integral definida.
Solo nos queda por ver un ejemplo de estos cálculos en nuestra carrera de ingeniería ambiental.
Aplicacion a la carrera
Integral Definida

Del tema anterior vimos que al hacer tender el valor de n al infinito podemos calcular el valor real del área que buscamos, esto corresponde a la integral definida, es decir, la integral como un límite. pero es necesario formalizar estas definiciones por lo que:
 Sea F definida en el intervalo cerrado [a,b] y sea delta una partición de [a,b] dada por
Sea F definida en el intervalo cerrado [a,b] y sea delta una partición de [a,b] dada por donde el delta de x es la longitud del í-esimo subintervalo. si c1 es cualquier punto del i-ésimo subintervalo, la suma:
donde el delta de x es la longitud del í-esimo subintervalo. si c1 es cualquier punto del i-ésimo subintervalo, la suma:
de donde partimos para la definición de la integral definida:
Si f está definida en el intervalo cerrado [a,b] y existe el límite:

Entonces f es integrable en [a,b] y el límite se denota como:

Este límite se conoce como la integral definida de f entre a y b. el numero a se llama límite inferior de integración y el numero b se llama límite superior de integración.
una vez hemos formalizado todo lo que hemos expresado anteriormente respecto al área es interesante definir las propiedades que cumplen este tipo de integrales y dar una definición más formal del area bajo la curva como la integral definida:
la integral definida como área de una región:
si f es contínua y no negativa en el intervalo cerrado [a,b], el área de la región limitada por la gráfica de f, el eje x y las rectas verticales x =a y x=b viene dada por:

y las propiedades que cumplen son:



En el próximo post veremos un video explicativo en donde encontraremos un ejemplo claro y detallado del cálculo de áreas mediante la integral definida.
continúa en Ejemplo
Cálculo del Área como límite

Si consideramos una región plana acotada por la grafica de una función y = f(x) siendo esta una función contínua y no negativa como en la figura de arriba, acotada tambien por el eje x y lateralmente por las rectas x = a y x = b podemos aplicar:
Dividiendo el intervalo [a, b] en n subintervalos, cada uno de longitud ∆x = (b-a)/n sus puntos terminales son:

Al ser f(x) contínua, el teorema de valores extremos asegura que exista un mínimo y un máximo de f(x) en cada sub intervalo. siendo:

Teniendo las 2 siguientes sumas:

de como lo vimos anteriormente, la suma por defecto es inferior a la suma por exceso, por lo que nuestra área real debajo de la función debe estar comprendida entre ambos valores de las sumas por defecto y por exceso.
Y si adicional a esto, hacemos que n (n = numero de particiones del segmento [a,b]) sea cada vez mayor, tendremos un área más aproximada, de lo cual podemos deducir que si hacemos que n tienda a infinito, entonces tendremos que:
Sea f continua y no negativa en el intervalo [a,b]. el área de la región limitada por la graica de f, el eje x y las rectas verticales x = a y x = b es:

siendo ∆x = (b-a)/n
Continúa en integral definida
Aplicación del tema

Una empresa que emite gases de efecto invernadero a la atmosfera necesita de un ingeniero ambiental para que controle los nocivos efectos de estos gases al ambiente, teniendo en cuenta la demanda de la industria así como el diagnostico que debe presentar a la autoridad ambiental.
En este diagnostico es pertinente presentar el trabajo realizado de la combustión de los gases de chimenea alterando los volúmenes de los gases iníciales como los gases finales para ellos es necesario utilizar la integral.

Donde el trabajo es el área bajo la curva.

Área de una región plana
Supongamos la gráfica de

Limitada por el eje x, entre x=0 y x=2.
Cuya gráfica corresponde a:



Vamos a utilizar el método del exhaución (arquímedes) para calcular el área comprendida entre la gráfica de f(x) y las rectas x=0 y x=5
Utilizaremos 5 rectángulos para aproximar el área de la región que corresponde a la imagen superior.
Primero utilizaremos rectángulos que aproximarán el área por defecto.
La base de cada rectángulo dibujado es 2/5 (puesto que hemos dividido 2 unidades en cinco partes iguales).
Los puntos terminales de la derecha en cada intervalo los podemos expresar como (2i / 5) , siendo i=1,2,3,4,5
La altura puede obtenerse evaluando f en el punto terminal derecho de cada intervalo
De manera más exacta, podemos expresar la suma de las áreas de los cinco rectángulos como:

Aquí vemos que la aproximación por defecto al área buscada utilizando los cinco rectángulos es 6.48 unidades cuadradas
Procedamos ahora a aproximar el área por exceso:

La base de cada rectángulo dibujado vuelve a ser 2/5 (puesto que hemos dividido 2 unidades en cinco partes iguales).
Ahora la altura de cada rectángulo viene dada por el valor de la función en cada punto terminal de la izquierda. siendo (2(i-1) / 5) , siendo i=1,2,3,4,5
El Área del i-ésimo rectángulo= 2/5 . f(2(i-1)/5)
La suma de todos los rectángulos vendrá dada por el sumatorio siguiente expresado en notación sigma:

Aquí vemos que la aproximación por exceso al área buscada utilizando los cinco rectángulos es 8.08 unidades cuadradas.
Podemos concluir que el Área de la región objeto de estudio está comprendida entre las dos medidas encontradas:
6.48 < Área de la región plana < 8.08
Si quisiéramos afinar la medición lo que tendremos que hacer será aumentar el nº de rectángulos, por ejemplo si utilizamos 25 rectángulos para aproximar la medición, tendríamos:
Área por defecto = 7.1712
Área por exceso = 7.4912
7.1712 < Área de la región plana < 7.4912
Continua en Cálculo del Área como límite
Área
En la geometría euclídea, la región plana más simple es el rectánmgulo. aunque suele decirse que la fórmula para el área del rectángulo es A = bh es más apropiado decir que eso es la definición del área del rectángulo.
De esa definición se puede deducir fórmulas para las áreas de otras regiones planas. Asi que para determinar el área de un triángulo, formamos un rectángulo de área doble y una vez hayada el área la dividimos en dos.
Cuando la región a hayar el área es no poligonal, es mucho más dificil. los griegos fueron capaces de encontrar formulas mediante el metodo de evaluación (debido a arquímedes) en el cual, el área se encierra en polígonos circunscritos como se muestra abajo y se calcula el valor del área de cada uno de ellos y posteriormente se suman todas esas áreas, llegando a una aproximación del área real que se debía calcular.

Usando un proceso análogo al de arquímedes calcularemos el área de regiones planas.
Continúa en Área de una región plana
Notación Sigma
| |
Esto se lee: Sumatorio sobre i, desde m hasta n, de x sub-i.
La variable i es el índice de suma al que se le asigna un valor inicial llamado límite inferior, m. La variable i recorrerá los valores enteros hasta alcanzar el límite superior, n. Necesariamente debe cumplirse que:
Si queremos expresar la suma de los cinco primeros números naturales podemos hacerlo de esta forma:
Algunos ejemplos adicionales:
Propiedades:
Fórmulas Interesantes: